Ι. Εισαγωγή
Το νερό μπορεί να ανάψει κεριά, είναι αλήθεια; Είναι αλήθεια!
Είναι αλήθεια ότι τα φίδια φοβούνται το realgar; Είναι ψέμα!
Αυτό που θα συζητήσουμε σήμερα είναι:
Οι παρεμβολές μπορούν να βελτιώσουν την ακρίβεια των μετρήσεων, ισχύει αυτό;
Υπό κανονικές συνθήκες, οι παρεμβολές είναι ο φυσικός εχθρός της μέτρησης. Οι παρεμβολές θα μειώσουν την ακρίβεια της μέτρησης. Σε σοβαρές περιπτώσεις, η μέτρηση δεν θα πραγματοποιηθεί κανονικά. Από αυτή την άποψη, οι παρεμβολές μπορούν να βελτιώσουν την ακρίβεια της μέτρησης, κάτι που είναι ψευδές!
Ωστόσο, ισχύει πάντα αυτό; Υπάρχει περίπτωση οι παρεμβολές να μην μειώνουν την ακρίβεια της μέτρησης, αλλά αντίθετα να τη βελτιώνουν;
Η απάντηση είναι ναι!
2. Συμφωνία Παρέμβασης
Σε συνδυασμό με την πραγματική κατάσταση, καταλήγουμε στην ακόλουθη συμφωνία σχετικά με την παρέμβαση:
- Οι παρεμβολές δεν περιέχουν στοιχεία συνεχούς ρεύματος. Στην πραγματική μέτρηση, οι παρεμβολές είναι κυρίως παρεμβολές εναλλασσόμενου ρεύματος και αυτή η υπόθεση είναι λογική.
- Σε σύγκριση με τη μετρούμενη τάση DC, το πλάτος της παρεμβολής είναι σχετικά μικρό. Αυτό συμφωνεί με την πραγματική κατάσταση.
- Η παρεμβολή είναι ένα περιοδικό σήμα ή η μέση τιμή είναι μηδέν εντός μιας καθορισμένης χρονικής περιόδου. Αυτό το σημείο δεν ισχύει απαραίτητα στην πραγματική μέτρηση. Ωστόσο, δεδομένου ότι η παρεμβολή είναι γενικά ένα σήμα AC υψηλότερης συχνότητας, για τις περισσότερες παρεμβολές, η σύμβαση του μηδενικού μέσου όρου είναι λογική για μεγαλύτερο χρονικό διάστημα.
3. Ακρίβεια μέτρησης υπό παρεμβολές
Τα περισσότερα ηλεκτρικά όργανα μέτρησης και μετρητές χρησιμοποιούν πλέον μετατροπείς AD και η ακρίβεια μέτρησης που προσφέρουν σχετίζεται στενά με την ανάλυση του μετατροπέα AD. Γενικά, οι μετατροπείς AD με υψηλότερη ανάλυση έχουν υψηλότερη ακρίβεια μέτρησης.
Ωστόσο, η ανάλυση του AD είναι πάντα περιορισμένη. Υποθέτοντας ότι η ανάλυση του AD είναι 3 bit και η υψηλότερη τάση μέτρησης είναι 8V, ο μετατροπέας AD ισοδυναμεί με μια κλίμακα διαιρούμενη σε 8 υποδιαιρέσεις, κάθε υποδιαίρεση είναι 1V. Το αποτέλεσμα μέτρησης αυτού του AD είναι πάντα ένας ακέραιος αριθμός και το δεκαδικό μέρος μεταφέρεται ή απορρίπτεται πάντα, το οποίο θεωρείται ότι μεταφέρεται σε αυτή την εργασία. Η μεταφορά ή η απόρριψη θα προκαλέσει σφάλματα μέτρησης. Για παράδειγμα, 6,3V είναι μεγαλύτερο από 6V και μικρότερο από 7V. Το αποτέλεσμα μέτρησης AD είναι 7V και υπάρχει σφάλμα 0,7V. Αυτό το σφάλμα ονομάζεται σφάλμα κβάντωσης AD.
Για την ευκολία της ανάλυσης, υποθέτουμε ότι η κλίμακα (μετατροπέας AD) δεν έχει άλλα σφάλματα μέτρησης εκτός από το σφάλμα κβαντοποίησης AD.
Τώρα, χρησιμοποιούμε δύο τέτοιες πανομοιότυπες κλίμακες για να μετρήσουμε τις δύο τάσεις DC που φαίνονται στο Σχήμα 1 χωρίς παρεμβολές (ιδανική κατάσταση) και με παρεμβολές.
Όπως φαίνεται στο Σχήμα 1, η πραγματική μετρούμενη τάση DC είναι 6,3V και η τάση DC στο αριστερό σχήμα δεν έχει καμία παρεμβολή και έχει σταθερή τιμή. Το σχήμα στα δεξιά δείχνει το συνεχές ρεύμα που διαταράσσεται από το εναλλασσόμενο ρεύμα και υπάρχει μια ορισμένη διακύμανση στην τιμή. Η τάση DC στο δεξιό διάγραμμα είναι ίση με την τάση DC στο αριστερό διάγραμμα μετά την εξάλειψη του σήματος παρεμβολής. Το κόκκινο τετράγωνο στο σχήμα αντιπροσωπεύει το αποτέλεσμα μετατροπής του μετατροπέα AD.

Ιδανική τάση DC χωρίς παρεμβολές
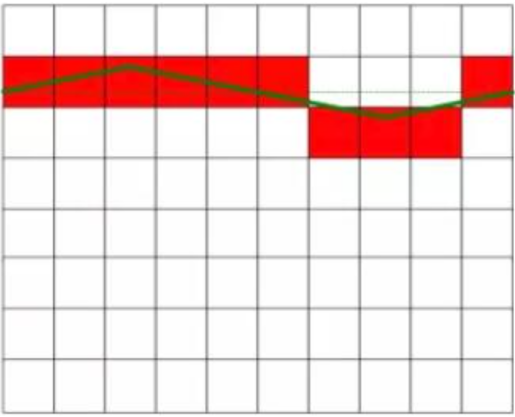
Εφαρμόστε μια παρεμβαλλόμενη τάση συνεχούς ρεύματος με μέση τιμή μηδέν
Πραγματοποιήστε 10 μετρήσεις του συνεχούς ρεύματος στις δύο περιπτώσεις του παραπάνω σχήματος και, στη συνέχεια, υπολογίστε τον μέσο όρο των 10 μετρήσεων.
Η πρώτη κλίμακα στα αριστερά μετριέται 10 φορές και οι μετρήσεις είναι οι ίδιες κάθε φορά. Λόγω της επίδρασης του σφάλματος κβαντισμού AD, κάθε ένδειξη είναι 7V. Μετά από 10 μετρήσεις, το αποτέλεσμα εξακολουθεί να είναι 7V. Το σφάλμα κβαντισμού AD είναι 0,7V και το σφάλμα μέτρησης είναι 0,7V.
Η δεύτερη κλίμακα στα δεξιά έχει αλλάξει δραματικά:
Λόγω της διαφοράς στο θετικό και αρνητικό της τάσης παρεμβολής και στο πλάτος, το σφάλμα κβάντωσης AD είναι διαφορετικό σε διαφορετικά σημεία μέτρησης. Με την αλλαγή του σφάλματος κβάντωσης AD, το αποτέλεσμα μέτρησης AD αλλάζει μεταξύ 6V και 7V. Επτά από τις μετρήσεις ήταν 7V, μόνο τρεις ήταν 6V, και ο μέσος όρος των 10 μετρήσεων ήταν 6,3V! Το σφάλμα είναι 0V!
Στην πραγματικότητα, κανένα σφάλμα δεν είναι αδύνατο, επειδή στον αντικειμενικό κόσμο, δεν υπάρχει αυστηρή τάση 6,3V! Ωστόσο, υπάρχουν πράγματι:
Σε περίπτωση μη παρεμβολής, καθώς το αποτέλεσμα κάθε μέτρησης είναι το ίδιο, μετά τον μέσο όρο 10 μετρήσεων, το σφάλμα παραμένει αμετάβλητο!
Όταν υπάρχει η κατάλληλη ποσότητα παρεμβολής, μετά τον υπολογισμό του μέσου όρου 10 μετρήσεων, το σφάλμα κβάντωσης AD μειώνεται κατά μία τάξη μεγέθους! Η ανάλυση βελτιώνεται κατά μία τάξη μεγέθους! Η ακρίβεια μέτρησης βελτιώνεται επίσης κατά μία τάξη μεγέθους!
Τα βασικά ερωτήματα είναι:
Είναι το ίδιο όταν η μετρούμενη τάση έχει άλλες τιμές;
Οι αναγνώστες ίσως θελήσουν να ακολουθήσουν τη συμφωνία σχετικά με τις παρεμβολές στη δεύτερη ενότητα, να εκφράσουν την παρεμβολή με μια σειρά αριθμητικών τιμών, να επικαλύψουν την παρεμβολή στην μετρούμενη τάση και στη συνέχεια να υπολογίσουν τα αποτελέσματα μέτρησης κάθε σημείου σύμφωνα με την αρχή μεταφοράς του μετατροπέα AD και στη συνέχεια να υπολογίσουν τη μέση τιμή για επαλήθευση, εφόσον το πλάτος παρεμβολής μπορεί να προκαλέσει αλλαγή στην ένδειξη μετά την κβαντοποίηση AD και η συχνότητα δειγματοληψίας είναι αρκετά υψηλή (οι αλλαγές πλάτους παρεμβολής έχουν μια διαδικασία μετάβασης, αντί για δύο τιμές θετικής και αρνητικής) και η ακρίβεια πρέπει να βελτιωθεί!
Μπορεί να αποδειχθεί ότι εφόσον η μετρούμενη τάση δεν είναι ακριβώς ακέραια (δεν υπάρχει στον αντικειμενικό κόσμο), θα υπάρχει σφάλμα κβάντωσης AD, ανεξάρτητα από το πόσο μεγάλο είναι το σφάλμα κβάντωσης AD, εφόσον το πλάτος της παρεμβολής είναι μεγαλύτερο από το σφάλμα κβάντωσης AD ή μεγαλύτερο από την ελάχιστη ανάλυση του AD, θα προκαλέσει αλλαγή στο αποτέλεσμα της μέτρησης μεταξύ δύο γειτονικών τιμών. Δεδομένου ότι η παρεμβολή είναι θετική και αρνητική συμμετρική, το μέγεθος και η πιθανότητα μείωσης και αύξησης είναι ίσα. Επομένως, όταν η πραγματική τιμή είναι πιο κοντά σε ποια τιμή, η πιθανότητα ποια τιμή θα εμφανιστεί είναι μεγαλύτερη και θα είναι κοντά σε ποια τιμή μετά τον υπολογισμό του μέσου όρου.
Δηλαδή: η μέση τιμή πολλαπλών μετρήσεων (η μέση τιμή παρεμβολής είναι μηδέν) πρέπει να είναι πιο κοντά στο αποτέλεσμα μέτρησης χωρίς παρεμβολές, δηλαδή, η χρήση του σήματος παρεμβολής AC με μέση τιμή μηδέν και ο υπολογισμός του μέσου όρου πολλαπλών μετρήσεων μπορεί να μειώσει τα ισοδύναμα σφάλματα κβαντισμού AD, να βελτιώσει την ανάλυση μέτρησης AD και να βελτιώσει την ακρίβεια μέτρησης!
Ώρα δημοσίευσης: 13 Ιουλίου 2023




